十进制二进制的算法 十进制转换为二进制的步骤

　　在计算机科学领域中，十进制和二进制是两种数字表示方式，十进制是我们日常生活中最常用的一种数字表示方法，而二进制则是计算机内部使用的一种数字表示方法。当需要将十进制数转换为二进制数时，我们需要遵循一定的算法和步骤。我们将十进制数从右向左不断除以2，直到商为0为止。每次除法的余数就是二进制数的一位，而商则是下一次除法的被除数。将得到的余数从下往上排列，即可得到对应的二进制数。这种算法和转换步骤的运用，为计算机内部的运算和存储提供了基础。

具体步骤：

1.方法一：

 1.正整数转二进制：除二取余，倒叙摆列，高位补零 

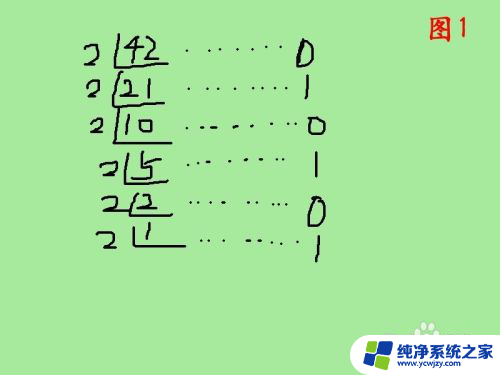
  即用2除正整数，从而得到商和余数；随后，用2除商，也将得到商与余数；如此重复，直至商小于1为止。然后，将余数进行倒叙摆列，从而得二进制。如图为十进制数20转二进制数

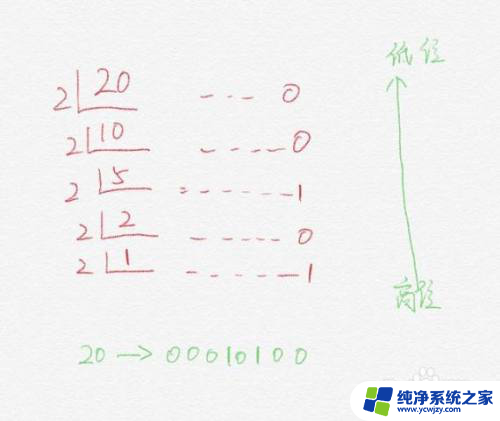
2.负整数转二进制：

  先将所对应的正整数转换为二进制，在对二进制数取反。然后对结果加一。如图为十进制数-20转换为二进制数

3.小数转二进制：乘2取整，正序排列

  对小数点后的小数乘2，得出结果后取整数。然后，继续利用小数乘2，如此重复，直至小数点后为0为止。如图为十进制数0.25转二进制

4.方法二：8421BCD码

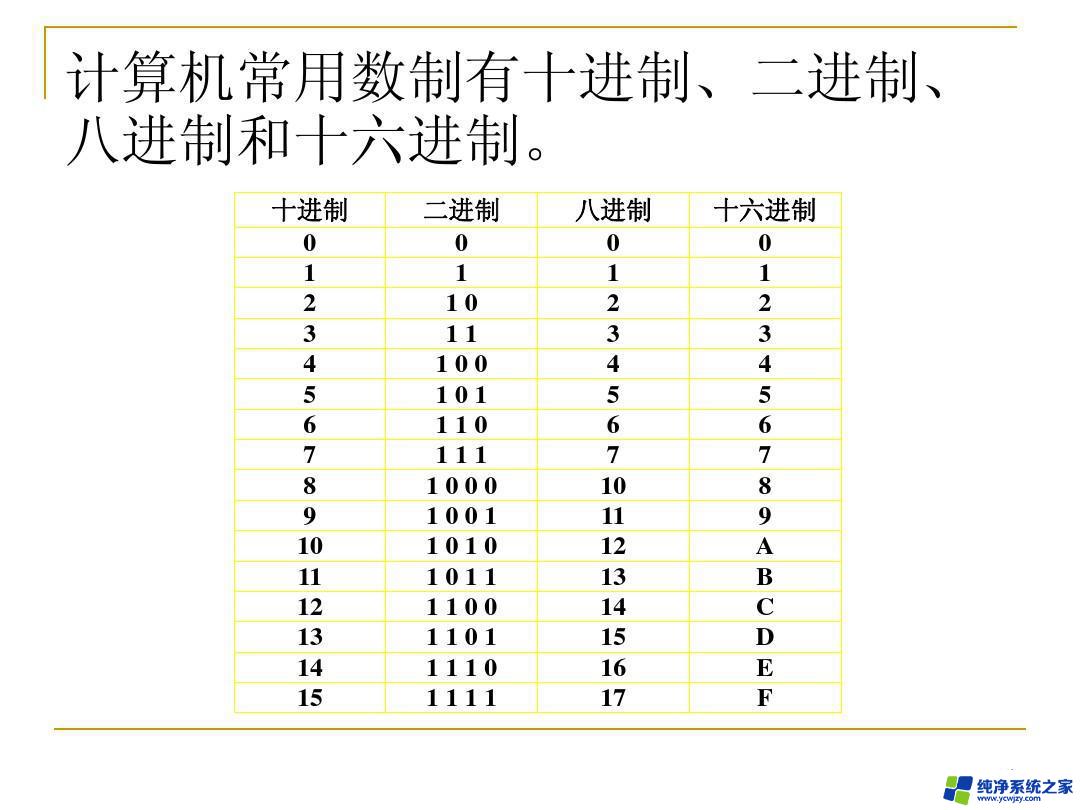
  8421码利用4为二进制码的组合来表示十进制数，且每一位二进制码的“1”代表为一个固定数值；通过对每位所对应的固定数值相加而得十进制数。如图，表示以8位二进制为例的每一位二进制码“1”所对应的固定数值。

5.  根据上图表中，以十进制80为例，进行详细讲解。8421码实质就是取对应二进制码“1”所对应的固定数值进行相加，使得等于目标的十进制数。对所取的对应固定数值的二进制位置1，未取得则置0，从而完成十进制到二进制的转换。

  十进制80对应上图固定值，它比128小，故取0；比64大，取1，则剩16；16比32小，取0；等于16 ，取1；而后续位均取0，从而得80的二进制为：01010000

　　以上就是十进制二进制的算法的全部内容，如果有任何疑问，用户可以按照我的方法来操作，希望这能对大家有所帮助。